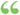 The perpendiculars from the vertices of a triangle to the opposite sides meet in a point. Let the Js be AH, BP, and CK. Through A, B, C suppose B'C', A'C', A'B', drawn II to BC, AC, AB, respectively. Then AH is _L to B'C'. (Why ?) Now ABCB' and A CBC'...  Vector Analysis: A Text-book for the Use of Students of Mathematics ... - Sivu 106tekijä(t) Edwin Bidwell Wilson, Josiah Willard Gibbs - 1901 - 436 sivuaKoko teos - Tietoja tästä kirjasta
 | William Chauvenet - 1893 - 340 sivua
...to the diagonals, they will form a parallelogram twice as large as the quadrilateral. 27. The three perpendiculars from the vertices of a triangle to the opposite sides meet in the same point. Suggestion. Draw through the three vertices lines parallel to the opposite sides of... | |
 | Seth Thayer Stewart - 1893 - 262 sivua
...known, l\ may be constructed, given length of secant — i chord ; whence length of secant is known. i3. The perpendiculars from the vertices of a triangle to the opposite sides are the bisectrices of the angles of the triangle formed by joining the feet of the perpendiculars.... | |
 | George Albert Wentworth, George Anthony Hill - 1894 - 150 sivua
...two adjacent angles of one are equal respectively to a side and two adjacent angles of the other. 2. The perpendiculars from the vertices of a triangle to the opposite sides meet in a common point. 3. The interior angle of a regular polygon exceeds the exterior angle by 120°. How many... | |
 | Wooster Woodruff Beman, David Eugene Smith - 1895 - 344 sivua
...from c and b, and .'. from a and b. Th. 30 8. .'. P1 lies on CT. Similarly for P4. Th. 30 Theorem 33. The perpendiculars from the vertices of a triangle to the opposite sides are concurrent. Given the A ABC. To prove that the perpendiculars from A, B, C, to a, b, c, respectively,... | |
 | Wooster Woodruff Beman, David Eugene Smith - 1895 - 346 sivua
...circumference passes through the feet of the perpendiculars from the other vertices to the opposite sides. 310. The perpendiculars from the vertices of a triangle to the opposite sides bisect the angles of the triangle formed by joining their feet ; the so-called Pedal Triangle. Theorem... | |
 | Andrew Wheeler Phillips, Irving Fisher - 1896 - 276 sivua
...likewise prove that it is also cut by the third median in the same point. Hence, etc. 145. Exercise. — The perpendiculars from the vertices of a triangle to the opposite sides meet in a point. Hint. — Draw through each vertex a parallel to the opposite side. Prove AE, BH, and CD are perpendicular... | |
 | Joe Garner Estill - 1896 - 168 sivua
...triangles are to each other as the squares of their homologous sides. Bowdoin College, June, 1895. 1. The perpendiculars from the vertices of a triangle to the opposite sides meet in a common point. 2. Upon a given straight line describe an arc of a circle which shall contain a given... | |
 | Joe Garner Estill - 1896 - 186 sivua
...triangles are to each other as the squares of their homologous sides. Bowdoin College, June, 1895. 1. The perpendiculars from the vertices of a triangle to the opposite sides meet in a common point. 2. Upon a given straight line describe an arc of a circle which shall contain a given... | |
 | Andrew Wheeler Phillips, Irving Fisher - 1896 - 276 sivua
...likewise prove that it is also cut by the third median in the same point. Hence, etc. 145. Exercise. — The perpendiculars from the vertices of a triangle to the opposite sides meet in a point. flint. — Draw through each vertex a parallel to the opposite side. Prove AE, BH, and CD are perpendicular... | |
 | Andrew Wheeler Phillips, Irving Fisher - 1896 - 276 sivua
...each parallel to and equal to half of BC. Then prove OE—ON—NC, and DO-OM=MB. 145. Exercise.—The perpendiculars from the vertices of a triangle to the opposite sides meet in a point. Hint.—Draw through each vertex a parallel to the opposite side. Prove AE, BH, and CD are perpendicular... | |
| |
