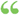 The perpendiculars from the vertices of a triangle to the opposite sides meet in a point. Let the Js be AH, BP, and CK. Through A, B, C suppose B'C', A'C', A'B', drawn II to BC, AC, AB, respectively. Then AH is _L to B'C'. (Why ?) Now ABCB' and A CBC'...  Vector Analysis: A Text-book for the Use of Students of Mathematics ... - Sivu 106tekijä(t) Edwin Bidwell Wilson, Josiah Willard Gibbs - 1901 - 436 sivuaKoko teos - Tietoja tästä kirjasta
 | George D. Pettee - 1896 - 272 sivua
...the sides of a triangle meet at a common point. CONCURRENT LINES PROPOSITION XXXV 47 120. Theorem. The perpendiculars from, the vertices of a triangle to the opposite sides 't"eet at a common point. E /G J K Appl. Prove J§ AD, BE, and CF are concurrent Cons. Through vertices... | |
 | Frederick Harold Bailey - 1897 - 392 sivua
...the axis of x. Then the vertices are (0, 0), (x,, 0), and (x 2 , y 2 )-) 96. Prove analytically that the perpendiculars from the vertices of a triangle to the opposite sides meet in a point. (Take axes as in Ex. 95.) 97. Prove analytically that the perpendiculars drawn from any two vertices... | |
 | Andrew Wheeler Phillips, Irving Fisher - 1897 - 374 sivua
...each other at right angles, and also bisect the angles of the rhombus. ' BOOK I 14:4:. Exercise.—The perpendiculars from the vertices of a triangle to the opposite sides meet in a point. Hint.—Draw through each vertex a parallel to the opposite side. Prove AE, BH, and CD are perpendicular... | |
 | Joe Garner Estill - 1897 - 168 sivua
...triangles are to each other as the squares of their homologous sides. Bowdoin College, June, 1895. 1. The perpendiculars from the vertices of a triangle to the opposite sides meet hi a common point. 2. Upon a given straight line describe an arc of a circle which shall contain a... | |
 | George Washington Hull - 1897 - 408 sivua
...opposite angles of a quadrilateral be supplementary, the quadrilateral can be inscribed in a circle. 576. The perpendiculars from the vertices of a triangle to the opposite sides are the bisectors of the angles of the triangle formed by joining the feet of the perpendiculars. 577.... | |
 | James Howard Gore - 1898 - 232 sivua
...is formed at each vertex of a triangle, their sum will be equal to four right angles. 3. Show that the perpendiculars from the vertices of a triangle to the opposite sides meet in a point. 4. Show that every point unequally distant from the sides of an angle lies outside of the bisector... | |
 | Yale University - 1898 - 212 sivua
...radius of the sphere of which it forms a part being ю feet. JUNE 1886. PLANE. 1. Prove that the three perpendiculars from the vertices of a triangle to the opposite sides meet in a point. 2. Two parallel chords or secants intercept equal arcs on a circumference. 3. The base of a triangle... | |
 | 1898 - 228 sivua
...radius of the sphere of which it forms a part being 10 feet. JUNE 1886. PLANE. 1. Prove that the three perpendiculars from the vertices of a triangle to the opposite sides meet in a point. 2. Two parallel chords or secants intercept equal arcs on a circumference. 3. The base of a triangle... | |
 | Webster Wells - 1898 - 264 sivua
...parallelogram form a rectangle. (By Ex. 46, each Z of EFGH is a rt. /..) B. PROP. LI. THEOREM. 138. The perpendiculars from the vertices of a triangle to the opposite sides intersect at a common point. Given AD, BE, and CFfhe Ja from the vertices of A ABC to the opposite... | |
 | George Albert Wentworth - 1899 - 272 sivua
...B. Hence, 0 is equidistant from B and C, and B therefore is in the _L bisector FF'. (Why ?) Ex. 26. The perpendiculars from the vertices of a triangle to the opposite sides meet in a point. Let the Js be AH, BP, and CK. Through A, B, C suppose B'C', A'fT, A'R, drawn II to BC, AC, AB, respectively.... | |
| |
