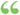 The perpendiculars from the vertices of a triangle to the opposite sides meet in a point. Let the Js be AH, BP, and CK. Through A, B, C suppose B'C', A'C', A'B', drawn II to BC, AC, AB, respectively. Then AH is _L to B'C'. (Why ?) Now ABCB' and A CBC'...  Vector Analysis: A Text-book for the Use of Students of Mathematics ... - Sivu 106tekijä(t) Edwin Bidwell Wilson, Josiah Willard Gibbs - 1901 - 436 sivuaKoko teos - Tietoja tästä kirjasta
 | William Frothingham Bradbury - 1877 - 262 sivua
...triangles, or an isosceles triangle can be added to it so as to form with it an isosceles triangle. 186. The perpendiculars from the vertices of a triangle to the opposite sides respectively bisect the angles of the triangle formed by joining the feet of these perpendiculars.... | |
 | Edward Albert Bowser - 1880 - 334 sivua
...tarry till he has mastered all the examples in any one article.] 1. Prove that the perpendiculars drawn from the vertices of a triangle to the opposite sides meet in a point. Let ABC be the triangle ; AF, BE, CD the perpendiculars. Assume AX and AY as the rectanguE « Fig. 38. lar axes ; and let the... | |
 | Elias Loomis - 1880 - 456 sivua
...three lines AD, BE, CF pass through the same point. PROPOSITION VI. 90. The three perpendiculars drawn from the vertices of a triangle to the opposite sides meet in a point. I.et ABC be a triangle, and let AD, BE, CF be drawn from the vertices perpendicular to the opposite... | |
 | William Frothingham Bradbury - 1880 - 260 sivua
...triangles, or an isosceles triangle can be added to it so as to form with it an isosceles triangle. 186i The perpendiculars from the vertices of a triangle to the opposite sides respectively bisect the angles of the triangle formed by joining the feet of these perpendiculars.... | |
 | George Albert Wentworth - 1881 - 266 sivua
...line is the -L erected at the middle oftliat line). QED PROPOSITION XXXVII. THEOREM. 121. The three perpendiculars from the vertices of a triangle to the opposite sides meet in a point. A' In the triangle ABC, let BP, AН, С К, be the perpendiculars from the vertices to the opposite... | |
 | Samuel Constable - 1882 - 222 sivua
...line drawn from A to the point D must pass through 0. Hence the three lines meet in a point. PROP. 21. The perpendiculars from the vertices of a triangle to the opposite sides meet in a point: and if a triangle be formed by joining their feet, its sides will be equally inclined to those of the... | |
 | Franklin Ibach - 1882 - 208 sivua
...¿— a = ¿— b ; and = AD=}AC. (63) (138) (45) (83) THEOREM XLIX. 143. The perpendiculars drawn from the vertices of a triangle to the opposite sides meet in a common point. • In the A ABC, let AD, BE, and С F be the _Ls from the vertices to the opposite sides.... | |
 | 1902 - 730 sivua
...— |- D But substituting a a + ar ar+ar» 1-fr 1+r 1+r 1. PLANE GEOMETRY. Answer any five. 1. Prove: The perpendiculars from the vertices of a triangle to the opposite sides meet in a common point. What is the name of this point? 2. A circle is inscribed in a triangle ABC. If D, E,... | |
 | Alfred Hix Welsh - 1883 - 326 sivua
...joining the adjacent middle points of the sides of a quadrilateral is a parallelogram. 10. The three perpendiculars from the vertices of a triangle to the opposite sides meet in the same point. Suggestion.—Through the vertices of the triangle draw parallels to the opposite sides;... | |
 | F. B. Stevens - 1884 - 202 sivua
...with respect to a point lying within and with respect to an axis cutting the triangle. 2. The three perpendiculars from the vertices of a triangle to the opposite sides meet in the same point. 3. To construct a polygon similar to a given polygon, the ratio of similitude of the... | |
| |
