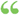 The perpendiculars from the vertices of a triangle to the opposite sides meet in a point. Let the Js be AH, BP, and CK. Through A, B, C suppose B'C', A'C', A'B', drawn II to BC, AC, AB, respectively. Then AH is _L to B'C'. (Why ?) Now ABCB' and A CBC'...  Vector Analysis: A Text-book for the Use of Students of Mathematics ... - Sivu 106tekijä(t) Edwin Bidwell Wilson, Josiah Willard Gibbs - 1901 - 436 sivuaKoko teos - Tietoja tästä kirjasta
 | United States. Office of Education - 1911 - 1154 sivua
...the tangent is a mean proportional between the whole secant and its external segment. 3. Prove that the perpendiculars from the vertices of a triangle to the opposite sides meet in a point. 4. Prove that the area of the triangle formed bj' joining the middle point of one of the non-parallel... | |
 | 1911 - 1030 sivua
...the tangent is a mean proportional between the whole secant and its external segment. 4. Prove that the perpendiculars from the vertices of a triangle to the opposite sides meet in a point. 5. The lengths of the circumferences of two concentric circles differ by 6 inches. Compute the width... | |
 | 1911 - 192 sivua
...1. Two and only two equal oblique lines can be drawn from a given point to a given straight line. 2. The perpendiculars from the vertices of a triangle to the opposite sides meet at a common point. 4. Define equal figures; equivalent figures; similar figures. Any two polygons are... | |
 | 1911 - 1096 sivua
...circumference to the sides arc collinear, the line being called Simson's line. We may here notice that the perpendiculars from the vertices of a triangle to the opposite sides are concurrent; their meet is called the orthocentre, and the triangle obtained by joining the feet... | |
 | George Albert Wentworth, David Eugene Smith - 1913 - 496 sivua
...lie with respect to the 0. bisector PP' ? This point O is called the circumcenter of the triangle. 4. The perpendiculars from the vertices of a triangle to the opposite sides are concurrent. Let the Ji be AQ, BR, and CP. Through A, B, C suppose B'C', C'A', and A'B' drawn II... | |
 | Edward Rutledge Robbins - 1915 - 282 sivua
...= 00° (104). .-. MB = BC (115). .-. AB, or 2 x J/fi, = 2 x CB (Ax. 6). PROPOSITION L. THEOREM 142. The perpendiculars from the vertices of a triangle to, the opposite sides meet in a point. .£s Given: A ABC, ^IX-Lto BC, Br-Lto AC, and CZ -Lto AB. To Prove : These three J§ meet in a point.... | |
 | John Wesley Young, Albert John Schwartz - 1915 - 250 sivua
...point of contact into segments which subtend equal angles at the point of contact of the circles. D 17. The perpendiculars from the vertices of a triangle to the opposite sides bisect the angles of the triangle formed by joining the feet. Describe circles on the three sides as... | |
 | Edward Rutledge Robbins - 1915 - 280 sivua
...for all positions of point P. [Draw BC. Prove tBCD, the ext ^ of £\PBC, ".. a constant. Etc.] 41. The perpendiculars from the vertices of a triangle to the opposite sides are the bisectors of the angles of the triangle formed by joining the feet of these perpendiculars.... | |
 | Frederick Shenstone Woods, Frederick Harold Bailey - 1917 - 536 sivua
...69. Prove analytically that the medians of a triangle meet in a point. 70. Prove analytically that the perpendiculars from the vertices of a triangle to the opposite sides meet in a point. 71. Prove analytically that the straight lines joining the middle points of the adjacent sides of any... | |
 | George Wentworth, David Eugene Smith, Joseph Clifton Brown - 1918 - 296 sivua
...about this joining line? \Vhere does 0 lie with respect to the J- bisector of the third side ? 15. The perpendiculars from the vertices of a triangle to the opposite sides are concurrent. , Given theJs-lQ, BR, and CP. Through \ R/ A, B, C draw B'C", C'A', and A'B' parallel... | |
| |
